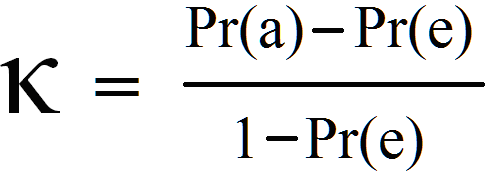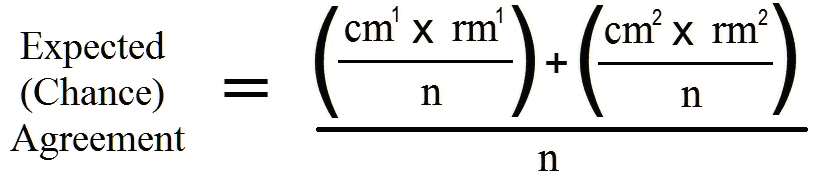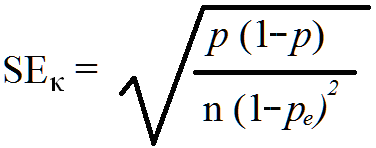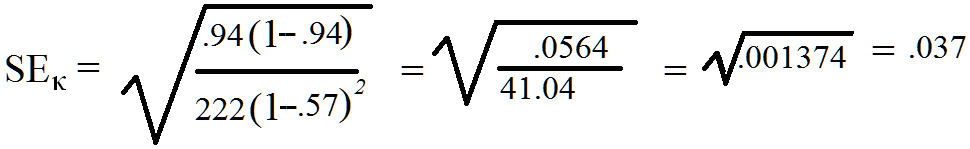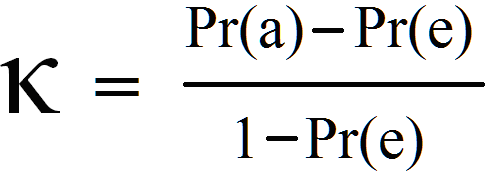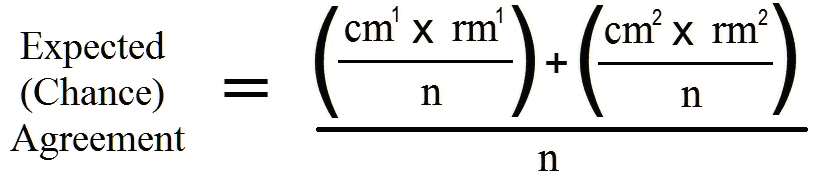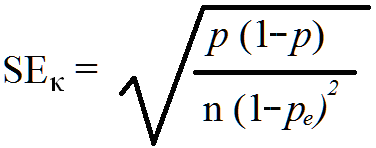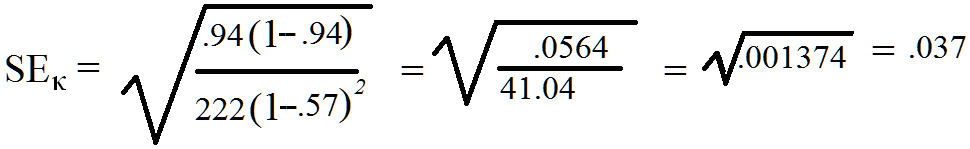Importance of measuring interrater reliability
Many situations in the healthcare industry rely on multiple people to collect research or clinical laboratory data. The question of consistency, or agreement among the individuals collecting data immediately arises due to the variability among human observers. Well-designed research studies must therefore include procedures that measure agreement among the various data collectors. Study designs typically involve training the data collectors, and measuring the extent to which they record the same scores for the same phenomena. Perfect agreement is seldom achieved, and confidence in study results is partly a function of the amount of disagreement, or error introduced into the study from inconsistency among the data collectors. The extent of agreement among data collectors is called, “interrater reliability”.
Interrater reliability is a concern to one degree or another in most large studies due to the fact that multiple people collecting data may experience and interpret the phenomena of interest differently. Variables subject to interrater errors are readily found in clinical research and diagnostics literature. Examples include studies of pressure ulcers (1,2) when variables include such items as amount of redness, edema, and erosion in the affected area. While data collectors may use measuring tools for size, color is quite subjective as is edema. In head trauma research, data collectors estimate the size of the patient’s pupils and the degree to which the pupils react to light by constricting. In the laboratory, people reading Papanicolaou (Pap) smears for cervical cancer have been found to vary in their interpretations of the cells on the slides (3). As a potential source of error, researchers are expected to implement training for data collectors to reduce the amount of variability in how they view and interpret data, and record it on the data collection instruments. Finally, researchers are expected to measure the effectiveness of their training and to report the degree of agreement (interrater reliability) among their data collectors.
Theoretical issues in measurement of rater reliability
Reliability of data collection is a component of overall confidence in a research study’s accuracy. The importance of technologists in a clinical laboratory having a high degree of consistency when evaluating samples is an important factor in the quality of healthcare and clinical research studies. There are many potential sources of error in any research project, and to the extent the researcher minimizes these errors, there can be confidence in the study’s findings and conclusions. In fact, the purpose of research methodology is to reduce to the extent possible, contaminants that may obscure the relationship between the independent and dependent variables. Research data are meaningful only when data collectors record data that accurately represent the state of the variables under observation.
There are actually two categories of reliability with respect to data collectors: reliability across multiple data collectors, which is interraterreliability, and reliability of a single data collector, which is termed intrarater reliability. With a single data collector the question is this: presented with exactly the same situation and phenomenon, will an individual interpret data the same and record exactly the same value for the variable each time these data are collected? Intuitively it might seem that one person would behave the same way with respect to exactly the same phenomenon every time the data collector observes that phenomenon. However, research demonstrates the fallacy of that assumption. One recent study of intrarater reliability in evaluating bone density X-Rays, produced reliability coefficients as low as 0.15 and as high as 0.90 (4). It is clear that researchers are right to carefully consider reliability of data collection as part of their concern for accurate research results.
Inter- and intrarater reliability are affected by the fineness of discriminations in the data that collectors must make. If a variable has only two possible states, and the states are sharply differentiated, reliability is likely to be high. For example, in a study of survival of sepsis patients, the outcome variable is either survived or did not survive. There are unlikely to be significant problems with reliability in collection of such data. On the other hand, when data collectors are required to make finer discriminations, such as the intensity of redness surrounding a wound, reliability is much more difficult to obtain. In such cases, the researcher is responsible for careful training of data collectors, and testing the extent to which they agree in their scoring of the variables of interest.
A final concern related to rater reliability was introduced by Jacob Cohen, a prominent statistician who developed the key statistic for measurement of interrater reliability, Cohen’s kappa (5), in the 1960s. Cohen pointed out that there is likely to be some level of agreement among data collectors when they do not know the correct answer but are merely guessing. He hypothesized that a certain number of the guesses would be congruent, and that reliability statistics should account for that random agreement. He developed the kappa statistic as a tool to control for that random agreement factor.
Measurement of interrater reliability
There are a number of statistics that have been used to measure interrater and intrarater reliability. A partial list includes percent agreement, Cohen’s kappa (for two raters), the Fleiss kappa (adaptation of Cohen’s kappa for 3 or more raters) the contingency coefficient, the Pearson r and the Spearman Rho, the intra-class correlation coefficient, the concordance correlation coefficient, and Krippendorff’s alpha (useful when there are multiple raters and multiple possible ratings). Use of correlation coefficients such as Pearson’s r may be a poor reflection of the amount of agreement between raters resulting in extreme over or underestimates of the true level of rater agreement (6). In this paper, we will consider only two of the most common measures, percent agreement and Cohen’s kappa.
Percent agreement
The concept of “agreement among raters” is fairly simple, and for many years interrater reliability was measured as percent agreement among the data collectors. To obtain the measure of percent agreement, the statistician created a matrix in which the columns represented the different raters, and the rows represented variables for which the raters had collected data (Table 1). The cells in the matrix contained the scores the data collectors entered for each variable. An example of this procedure can be found in Table 1. In this example, there are two raters (Mark and Susan). They each recorded their scores for variables 1 through 10. To obtain percent agreement, the researcher subtracted Susan’s scores from Mark’s scores, and counted the number of zeros that resulted. Dividing the number of zeros by the number of variables provides a measure of agreement between the raters. In Table 1, the agreement is 80%. This means that 20% of the data collected in the study is erroneous because only one of the raters can be correct when there is disagreement. This statistic is directly interpreted as the percent of data that are correct. The value, 1.00 - percent agreement may be understood as the percent of data that are incorrect. That is, if percent agreement is 82, 1.00-0.82 = 0.18, and 18% is the amount of data misrepresents the research data.
Table 1. Calculation of percent agreement (fictitious data).
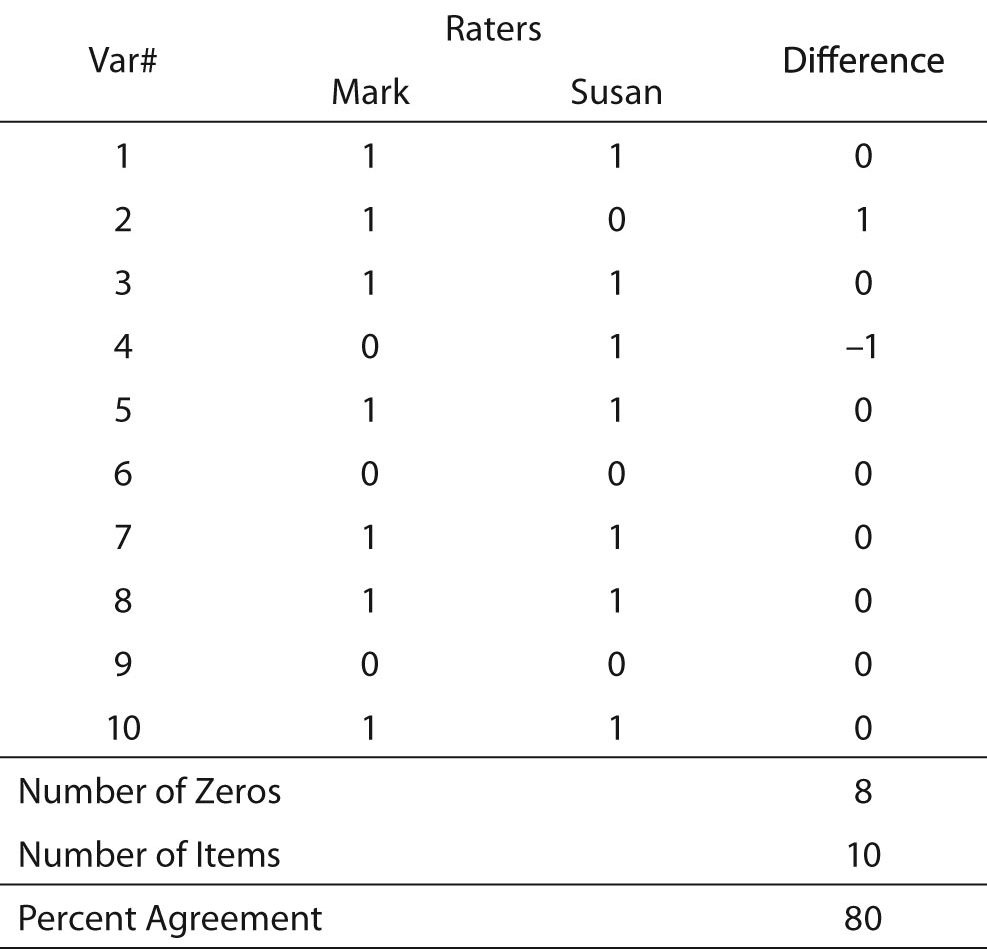
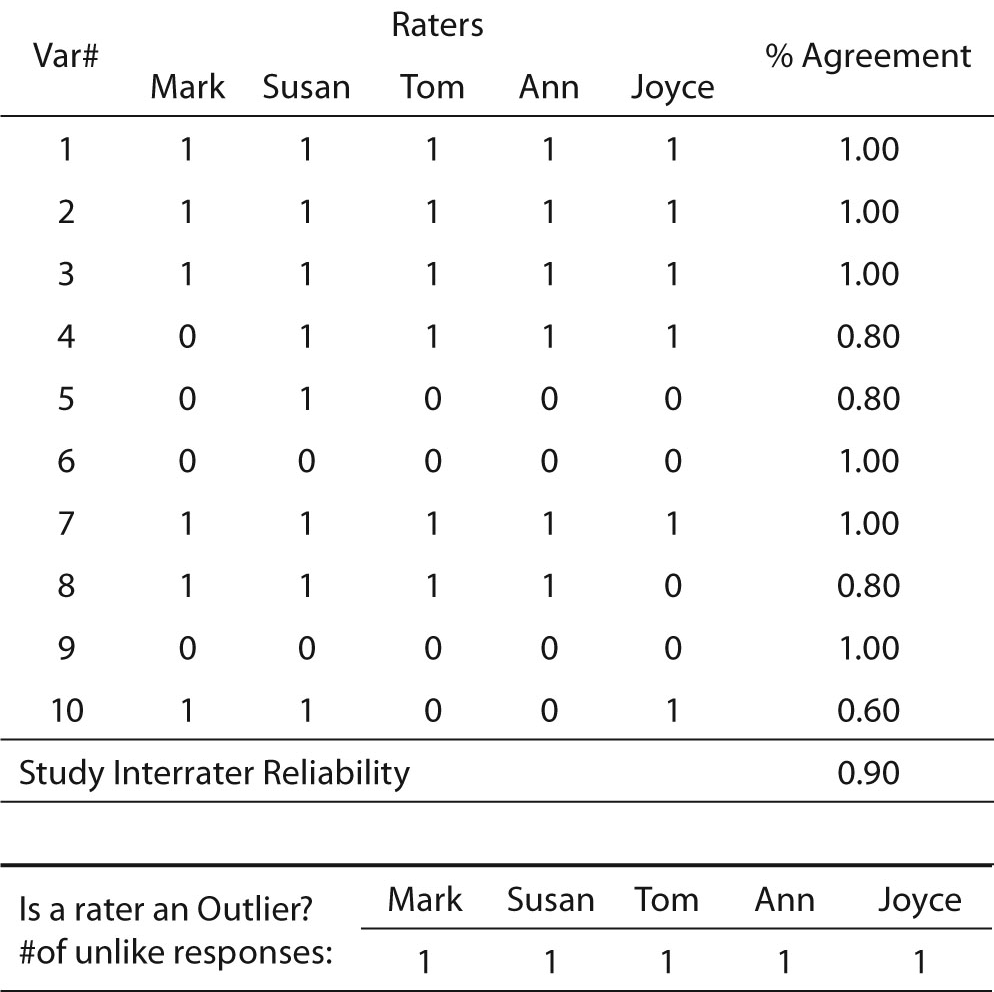
This is a simple procedure when the values consist only of zero and one, and the number of data collectors is two. When there are more data collectors, the procedure is slightly more complex (Table 2). So long as the scores are limited to only two values, however, calculation is still simple. The researcher merely calculates the percent agreement for each row and averages the rows. Another benefit of the matrix is that it permits the researcher to discover if errors are random and thus fairly evenly distributed across all raters and variables, or if a particular data collector frequently records values different from the other data collectors. In Table 2, which exhibits an overall interrater reliability of 90%, it can be seen that no data collector had an excessive number of outlier scores (scores that disagreed with the majority of raters’ scores). Another benefit of this technique is that it allows the researcher to identify variables that may be problematic. Note that Table 2 shows that the raters achieved only 60% agreement for Variable 10. This variable may warrant scrutiny to identify the cause of such low agreement in its scoring.
Table 2. Percent agreement across multiple data collectors (fictitious data).
So far, the discussion has made an assumption that the majority were correct, and that the minority raters were incorrect in their scores, and that all raters made a deliberate choice of a rating. Jacob Cohen recognized that assumption may be false. In fact, he specifically noted: “In the typical situation, there is no criterion for the ‘correctness’ of judgments” (5). Cohen suggests the possibility that for at least some of the variables, none of the raters were sure what score to enter and simply made random guesses. In that case, the achieved agreement is a false agreement. Cohen’s kappa was developed to account for this concern.
Cohen’s kappa
Cohen’s kappa, symbolized by the lower case Greek letter, κ (7) is a robust statistic useful for either interrater or intrarater reliability testing. Similar to correlation coefficients, it can range from -1 to +1, where 0 represents the amount of agreement that can be expected from random chance, and 1 represents perfect agreement between the raters. While kappa values below 0 are possible, Cohen notes they are unlikely in practice (8). As with all correlation statistics, the kappa is a standardized value and thus is interpreted the same across multiple studies.
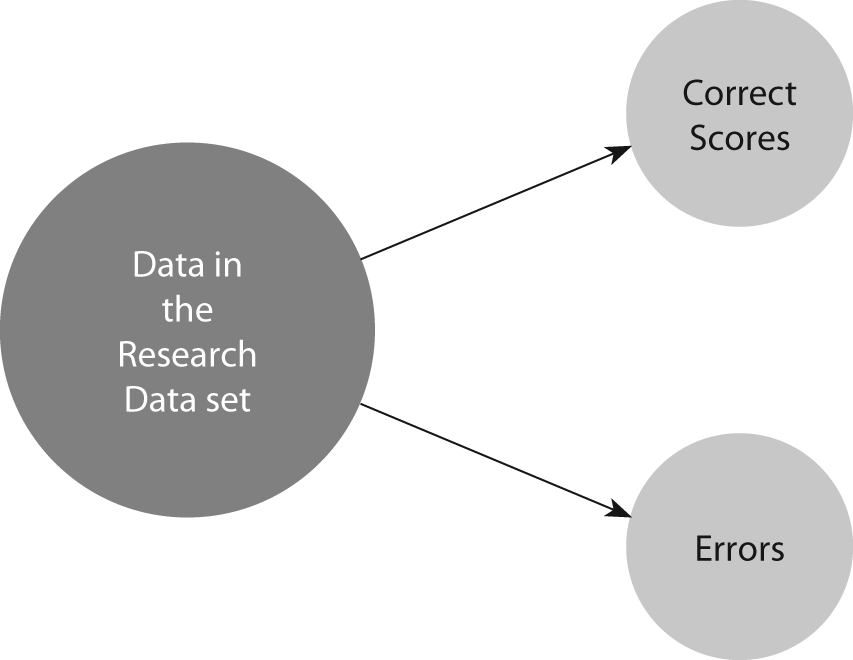
Cohen suggested the Kappa result be interpreted as follows: values ≤ 0 as indicating no agreement and 0.01–0.20 as none to slight, 0.21–0.40 as fair, 0.41–0.60 as moderate, 0.61–0.80 as substantial, and 0.81–1.00 as almost perfect agreement. However, this interpretation allows for very little agreement among raters to be described as “substantial”. For percent agreement, 61% agreement can immediately be seen as problematic. Almost 40% of the data in the dataset represent faulty data. In healthcare research, this could lead to recommendations for changing practice based on faulty evidence. For a clinical laboratory, having 40% of the sample evaluations being wrong would be an extremely serious quality problem. This is the reason that many texts recommend 80% agreement as the minimum acceptable interrater agreement. Given the reduction from percent agreement that is typical in kappa results, some lowering of standards from percent agreement appears logical. However, accepting 0.40 to 0.60 as “moderate” may imply the lowest value (0.40) is adequate agreement. A more logical interpretation is suggested in Table 3. Keeping in mind that any agreement less than perfect (1.0) is a measure not only of agreement, but also of the reverse, disagreement among the raters, the interpretations in Table 3 can be simplified as follows: any kappa below 0.60 indicates inadequate agreement among the raters and little confidence should be placed in the study results. Figure 1 displays the concept of research datasets as consisting of both correct and incorrect data. For Kappa values below zero, although unlikely to occur in research data, when this outcome does occur it is an indicator of a serious problem. A negative kappa represents agreement worse than expected, or disagreement. Low negative values (0 to -0.10) may generally be interpreted as “no agreement”. A large negative kappa represents great disagreement among raters. Data collected under conditions of such disagreement among raters are not meaningful. They are more like random data than properly collected research data or quality clinical laboratory readings. Those data are unlikely to represent the facts of the situation (whether research or clinical data) with any meaningful degree of accuracy. Such a finding requires action to either retrain raters or redesign the instruments.
Table 3. Interpretation of Cohen’s kappa.
Figure 1. Components of data in a research data set.
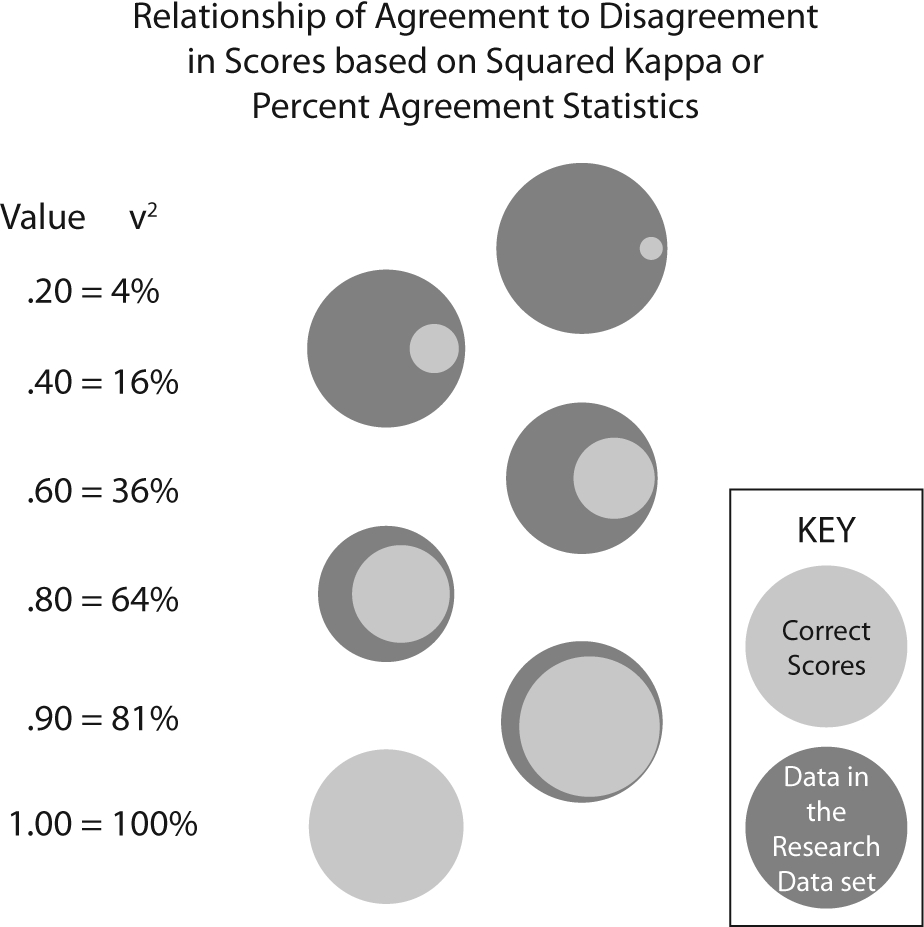
The kappa is a form of correlation coefficient. Correlation coefficients cannot be directly interpreted, but a squared correlation coefficient, called the coefficient of determination (COD) is directly interpretable. The COD is explained as the amount of variation in the dependent variable that can be explained by the independent variable. While the true COD is calculated only on the Pearson r, an estimate of variance accounted for can be obtained for any correlation statistic by squaring the correlation value. By extension, the squaring the kappa translates conceptually to the amount of accuracy (i.e. the reverse of error) in the data due to congruence among the data collectors. Figure 2 displays an estimate of the amount of correct and incorrect data in research data sets by the level of congruence as measured by either percent agreement or kappa.
Figure 2. Graphical representation of amount of correct data by % agreement or squared kappa value.
As noted by Marusteri and Bacarea (9), there is never 100% certainty about research results, even when statistical significance is achieved. Statistical results for testing hypotheses about the relationship between independent and dependent variables become meaningless if there is inconsistency in how raters score the variables. When agreement is less than 80%, over 20% of the data being analyzed are erroneous. For reliability of only 0.50 to 0.60, it must be understood that means that 40% to 50% of the data being analyzed are erroneous. When kappa values are below 0.60, the confidence intervals about the obtained kappa are sufficiently wide that one can surmise that about half the data may be incorrect (10). Clearly, statistical significance means little when so much error exists in the results being tested.
Calculation of Cohen’s kappa may be performed according to the following formula:
Where Pr(a) represents the actual observed agreement, and Pr(e) represents chance agreement.
Note that the sample size consists of the number of observations made across which raters are compared. Cohen specifically discussed two raters in his papers. The kappa is based on the chi-square table, and the Pr(e) is obtained through the following formula:
where: cm1 represents column 1 marginal
cm2 represents column 2 marginal
rm1 represents row 1 marginal,
rm2 represents row 2 marginal, and
n represents the number of observations (not the number of raters).
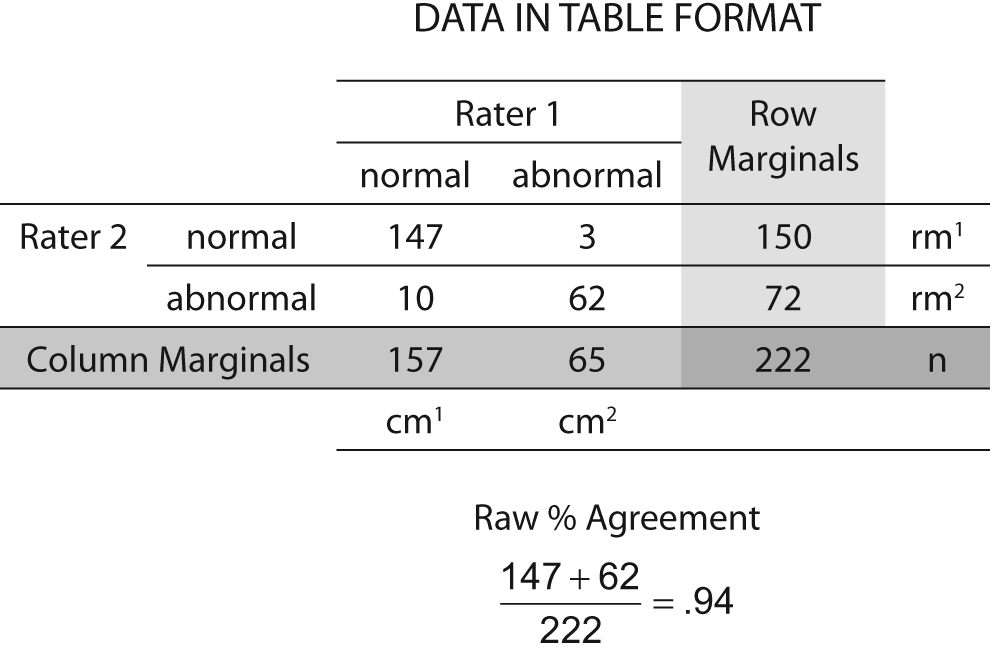
An example of the kappa statistic calculated may be found in Figure 3. Notice that the percent agreement is 0.94 while the Kappa is 0.85 — a considerable reduction in the level of congruence. The greater the expected chance agreement, the lower the resulting value of the kappa.
Figure 3. Data for kappa calculation example.
Unfortunately, marginal sums may or may not estimate the amount of chance rater agreement under uncertainty. Thus, it is questionable whether the reduction in the estimate of agreement provided by the kappa statistic is actually representative of the amount of chance rater agreement. Theoretically, Pr(e) is an estimate of the rate of agreement if the raters guessed on every item, and guessed at rates similar to marginal proportions, and if raters were entirely independent (11). None of these assumptions is warranted, and thus there is much disparity of opinion about the use of the Kappa among researchers and statisticians.
A good example of the reason for concern about the meaning of obtained kappa results is exhibited in a paper that compared human visual detection of abnormalities in biological samples with automated detection (12). Findings demonstrated only moderate agreement between the human versus the automated raters for the kappa (κ = 0.555), but the same data produced an excellent percent agreement of 94.2%. The problem of interpreting these two statistics’ results is this: how shall researchers decide if the raters reliable or not? Are the obtained results indicative of the great majority of patients receiving accurate laboratory results and thus correct medical diagnoses or not? In the same study, the researchers selected one data collector as the standard and compared five other technicians’ results with the standard. While data sufficient to calculate a percent agreement are not provided in the paper, the kappa results were only moderate. How shall the laboratory director know if the results represent good quality readings with only a small amount of disagreement among the trained laboratory technicians, or if a serious problem exists and further training is needed? Unfortunately, the kappa statistic does not provide enough information to make such a decision. Furthermore, a kappa may have such a wide confidence interval (CI) that it includes anything from good to poor agreement.
Confidence intervals for kappa
Once the kappa has been calculated, the researcher is likely to want to evaluate the meaning of the obtained kappa by calculating confidence intervals for the obtained kappa. The percent agreement statistic is a direct measure and not an estimate. There is therefore little need for confidence intervals. The kappa is, however, an estimate of interrater reliability and confidence intervals are therefore of more interest.
Theoretically, the confidence intervals are represented by subtracting from kappa from the value of the desired CI level times the standard error of kappa. Given that the most frequent value desired is 95%, the formula uses 1.96 as the constant by which the standard error of kappa (SEκ) is multiplied. The formula for a confidence interval is:
κ - 1.96 x SEκ to κ + 1.96 x SEκ
To obtain the standard error of kappa (SEκ) the following formula should be used:
Thus, the standard error of kappa for the data in Figure 3, P = 0.94, pe = 0.57, and N = 222
For the Figure 3 data, Kappa = .85 with a 95% Confidence Interval is calculated as follows:
0.85 - 1.96 x 0.037 to 0.85 + 1.96 x 0.037, which calculates to an interval of 0.77748 to 0.92252 which rounds to a confidence interval of 0.78 to 0.92. It should be noted that the SEκ is partially dependent upon sample size. The larger the number of observations measured, the smaller the expected standard error. While the kappa can be calculated for fairly small sample sizes (e.g. 5), the CI for such studies is likely to be quite wide resulting in “no agreement” being within the CI. As a general heuristic, sample sizes should not consist of less than 30 comparisons. Sample sizes of 1,000 or more are mathematically most likely to produce very small CIs, which means the estimate of agreement is likely to be very precise.
Figure 4. Calculation of the kappa statistic.
Conclusions
Both percent agreement and kappa have strengths and limitations. The percent agreement statistic is easily calculated and directly interpretable. Its key limitation is that it does not take account of the possibility that raters guessed on scores. It thus may overestimate the true agreement among raters. The kappa was designed to take account of the possibility of guessing, but the assumptions it makes about rater independence and other factors are not well supported, and thus it may lower the estimate of agreement excessively. Furthermore, it cannot be directly interpreted, and thus it has become common for researchers to accept low kappa values in their interrater reliability studies. Low levels of interrater reliability are not acceptable in health care or in clinical research, especially when results of studies may change clinical practice in a way that leads to poorer patient outcomes. Perhaps the best advice for researchers is to calculate both percent agreement and kappa. If there is likely to be much guessing among the raters, it may make sense to use the kappa statistic, but if raters are well trained and little guessing is likely to exist, the researcher may safely rely on percent agreement to determine interrater reliability.